Researchers at Northwestern University have discovered that structural features of the brain are close to a critical point similar to a phase transition, seen in various species such as humans, mice and fruit flies. This discovery suggests that a universal principle could govern the structure of the brain, which could inspire new computational models to mimic the complexity of the brain.
The brain exhibits structural criticality near phase transitions, constant across
” data-gt-translate-attributes=”({“attribute”:”data-cmtooltip”, “format”:”html”})” tabindex=”0″ role=”link”>speciespotentially guiding the development of new brain models.
When a magnet is heated, it reaches a critical point where it loses its magnetization, called “criticality”. This point of great complexity is reached when a physical object undergoes a phase transition.
Recently, researchers from
” data-gt-translate-attributes=”({“attribute”:”data-cmtooltip”, “format”:”html”})” tabindex=”0″ role=”link”>Northwestern University found that structural features of the brain lie near a similar critical point, either at or near a structural phase transition. These results are consistent in the brains of humans, mice and fruit flies, suggesting that this finding may be universal. Although it remains unclear between which phases brain structure evolves, these results could enable new designs of computational models of brain complexity.
Their research was published in Physics of communications.
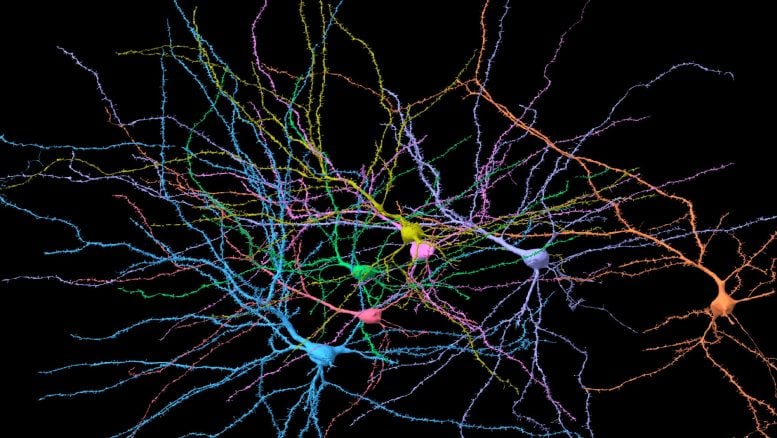
3D reconstruction of selected neurons in a small region of the human cortex dataset. Credit: Harvard University/Google
Brain structure and computer models
“The human brain is one of the most complex systems known, and many properties of the details governing its structure are not yet understood,” said lead author István Kovács, assistant professor of physics and astronomy at Northwestern. .
“Several other researchers have studied the criticality of the brain in terms of neuronal dynamics. But we study criticality at the structural level in order, ultimately, to understand how it underlies the complexity of brain dynamics. It’s a missing piece in our way of thinking about the complexity of the brain. Unlike a computer where any software can run on the same hardware, in the brain, dynamics and hardware are closely linked.

3D reconstruction of selected neurons in a small region of the human cortex dataset. Credit: Harvard University/Google
“The structure of the brain at the cellular level appears to be close to a phase transition,” said first author Helen Ansell, a Tarbutton fellow at Emory University and a postdoctoral researcher in Kovács’ lab during the study. “An everyday example of this is the fusion of ice and water. They are still water molecules, but they undergo a transition from solid to liquid. We are certainly not saying that the brain is about to melt. In fact, we have no way of knowing which two phases the brain might pass between. Because if it were on either side of the critical point, it wouldn’t be a brain. »
Applying statistical physics to neuroscience
Although researchers have long studied brain dynamics using functional magnetic resonance imaging (
” data-gt-translate-attributes=”({“attribute”:”data-cmtooltip”, “format”:”html”})” tabindex=”0″ role=”link”>fMRI) and electroencephalograms (EEG), advances in neuroscience have only recently provided massive data sets on the cellular structure of the brain. These data opened up the possibility for Kovács and his team to apply statistical physics techniques to measure the physical structure of neurons.

Snapshot of selected neurons from the human cortex dataset, visualized using the online Neuroglancer platform. Credit: Harvard University/Google
Identify critical exponents in brain structure
Kovács and Ansell analyzed publicly available data from 3D brain reconstructions of humans, fruit flies and mice. By examining the brain
” data-gt-translate-attributes=”({“attribute”:”data-cmtooltip”, “format”:”html”})” tabindex=”0″ role=”link”>nanoscale resolution, the researchers found that the samples exhibited physical property characteristics associated with criticality.
One of these properties is the well-known fractal-like structure of neurons. This non-trivial fractal dimension is an example of a set of observables, called “critical exponents”, that emerge when a system is close to a phase transition.
Brain cells are arranged in a fractal-like statistical pattern at different scales. When zoomed in, the fractal shapes are “self-similar,” meaning that smaller parts of the sample resemble the entire sample. The sizes of the different neuronal segments observed are also diverse, which provides another clue. According to Kovács, self-similarity, long-range correlations, and broad size distributions are all signatures of a critical state, where features are neither too organized nor too random. These observations lead to a set of critical exponents that characterize these structural features.
“These are things we see in all critical systems in physics,” Kovács said. “It appears that the brain is in a delicate balance between two phases.”
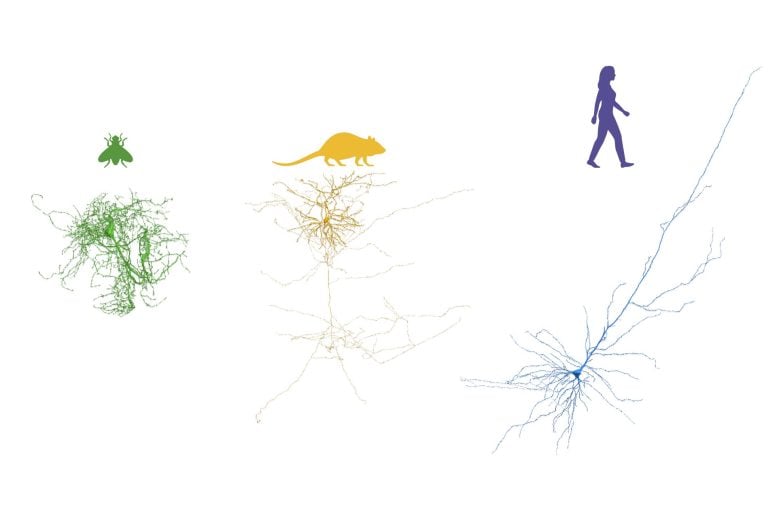
Examples of single neuron reconstruction from each of the fruit fly, mouse, and human datasets. Credit: Northwestern University
Universal criticality for all species
Kovács and Ansell were surprised to find that all the brain samples studied – from humans, mice and fruit flies – had consistent critical exponents across organisms, meaning they share the same quantitative criticality characteristics. The underlying, compatible structures between organisms suggest that a universal governing principle may be at play. Their new findings could potentially help explain why the brains of different creatures share some of the same fundamental principles.
“Initially, these structures appear very different: an entire fly brain is about the size of a small human neuron,” Ansell said. “But then we discovered surprisingly similar emergent properties.”
“Among the many very different characteristics among organisms, we relied on suggestions from statistical physics to check which measurements are potentially universal, such as critical exponents. Indeed, these are consistent across organisms,” said Kovács. “An even deeper sign of criticality, the critical exponents obtained are not independent: from any three, we can calculate the remainder, as statistical physics dictates. This discovery paves the way for formulating simple physical models to capture statistical patterns of brain structure. Such models provide useful inputs for dynamic brain models and can be a source of inspiration for artificial neural network architectures.
In the future, the researchers plan to apply their techniques to new and emerging datasets, including larger sections of the brain and more organisms. They aim to determine whether universality will still apply.
Reference: “Unveiling universal aspects of brain cellular anatomy” by Helen S. Ansell and István A. Kovács, June 10, 2024, Physics of communications.
DOI: 10.1038/s42005-024-01665-y
Funding: This study was partially supported by computing resources at Northwestern’s Quest High Performance Computing Facility.