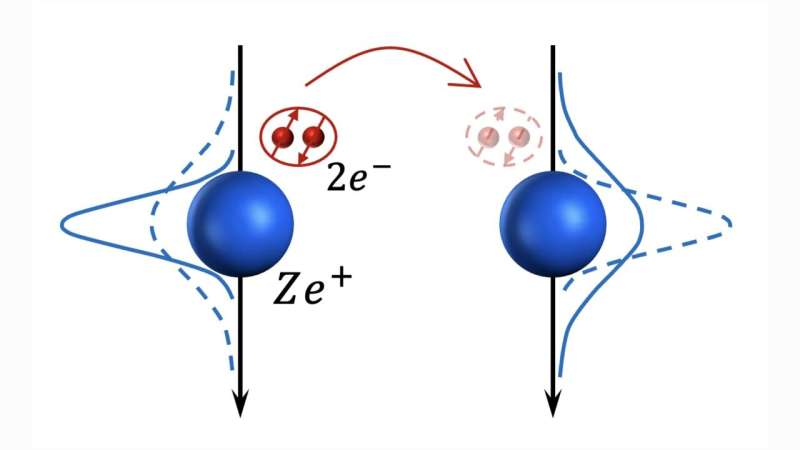
Conceptual image of the formation of quantum bipolarons. The blue spheres represent the positively charged ions in the material’s lattice and the two red dots the Cooper pairs. Credit: Pavel A. Volkov.
A new study published in Physical Examination Letters (PRL) explores the potential of quadratic electron-phonon coupling to enhance superconductivity through the formation of quantum bipolarons.
Electron-phonon coupling is the interaction between electrons and vibrations in a network called phonons. This interaction is crucial for the superconductivity (electrical conductance without resistance) of certain materials because it facilitates the formation of Cooper pairs.
Cooper pairs are pairs of electrons linked together via attractive interactions. When these Cooper pairs condense into a coherent state, we obtain superconducting properties.
Electron-phonon coupling can be classified based on its dependence on phonon displacement, that is, the intensity of lattice vibrations. The most commonly considered case is where the electron density couples linearly to lattice displacements, causing distortion of the lattice around each electron.
The researchers wanted to study whether superconductivity could be enhanced for materials exhibiting quadratic coupling, that is, when the interaction energy is proportional to the square of the phonon displacement.
Phys.org spoke with study co-authors Zhaoyu Han, a Ph.D. candidate at Stanford University and Dr. Pavel Volkov, assistant professor in the Department of Physics at the University of Connecticut.
Speaking about his motivation behind pursuing this research, Han said: “It was one of my dreams to identify and propose new mechanisms that could help achieve high-temperature superconductivity.”
Dr Volkov said: “The superconductivity of doped strontium titanate was discovered over 50 years ago, however, its mechanism remains an open question, with conventional mechanisms unlikely. This is why I started looking for alternative electron-phonon coupling mechanisms.
Linear coupling and its challenges for superconductivity
As mentioned earlier, coupling can be classified as linear or quadratic coupling.
Linear coupling refers to the scenario in which the coupling is proportional to the displacement of the phonons. On the other hand, the quadratic coupling depends on the square of the phonon displacement.
They can be identified by studying material symmetry, experimental observations and theoretical frameworks. Their implications for superconductivity, however, seem very different.
Linear coupling, observed in most superconducting materials, is widely studied due to its prevalence in many materials and has a theoretical framework.
However, conventional superconductors with linear electron-phonon coupling face limitations. These materials have a low critical temperature, which is the temperature below which the material can exhibit superconductivity.
Han explained: “The critical temperatures for these superconductors are generally below 30 Kelvin or -243.15 degrees Celsius. This is partly because the Cooper pair binding energy and kinetic energy are exponentially suppressed in the weak and strong coupling regimes, respectively. »
In weak coupling, electron-phonon interactions are weak due to low binding energy. In case of strong coupling, the interactions are stronger, leading to a higher effective mass of the Cooper pairs, thereby suppressing superconductivity.
However, the suppression hampers any effort to improve critical temperatures in such materials by simply increasing the coupling strength, encouraging researchers to explore materials with quadratic electron-phonon coupling, which are not as well understood.
Holstein model and quantum bipolarons
The Holstein model is a theoretical framework used to describe the interaction between electrons and phonons. It has already been used to study the generic physics of linear electron-phonon coupling.
The researchers extended the Holstein model to incorporate quadratic electron-phonon coupling into their study.
The Holstein model allows the calculation of quantities such as the binding energy of Cooper pairs and the critical temperature of superconductors.
In conventional materials, phonon-mediated electron binding leads to the formation of Cooper pairs.
The interaction is linear, which means that the strength of the coupling increases with the amplitude of the network vibrations. This interaction can be understood using classical physics principles and is well supported by experimental observations such as isotope effects.
In the case of quadratic coupling, it is totally different. By extending the Holstein model to incorporate the second-order dependence of coupling on phonon motion, researchers account for quantum fluctuations (random motion) of phonons and zero-point energy (the energy of phonons at 0 Kelvin). .
The electrons interact with the quantum fluctuations of the phonons, forming “quantum bipolarons”. Unlike linear coupling, the origin of attractive interactions is purely quantum mechanical.
Superconductivity at weak and strong coupling limit
The researchers found that when the electron-phonon interaction is weak, the mechanism by which electrons pair to form Cooper pairs is not efficient, as in the linear case. This leads to a low critical temperature which can be affected by the mass of the ions (isotope effect), but in a different way than in the linear case.
In other words, the (low) critical temperature of the material can change significantly depending on different atomic masses.
On the other hand, when electron-phonon interactions are strong, we obtain the formation of quantum bipolarons, which can become superconductors at a temperature fixed by their effective mass and density.
Below the critical temperature, the condensate of quantum bipolarons can move freely without disturbing the crystal. Greater mobility leads to a superconducting state, which is more stable and has a higher critical temperature. Unlike the linear mechanism, the mass of the quantum bipolaron is only slightly enhanced by the coupling, allowing higher critical temperatures.
“Our work demonstrates that this mechanism allows higher transition temperatures, at least for strong coupling. What is also positive is that this mechanism does not require any special preconditions to operate, and there are conditions quite realistic facts in which he will be dominant,” explained Dr. Volkov.
Han predicted: “Based on the fundamental physical constants relevant to solid materials, an optimistic estimate of the critical temperature achievable by this mechanism may be on the order of 100 Kelvin. »
Future work
“The potential implication would be above all an increase in the superconducting transition temperature. Superconductivity also depends sensitively on the properties of the electrons. Thus, to obtain strong coupling, we propose to use superlattices specially designed for electrons,” explained Dr. Volkov.
The researchers mention that, in theory, the next step would be to find the optimal coupling force regime for superconductivity. The researchers also hope that experimentalists will explore superlattice materials with large quadratic electron-phonon couplings.
“Experimentally, creating superlattices via patterning or using interfaces between twisted materials could be a promising route to achieving the kind of superconductivity we predicted,” Dr Volkov said.
Han also emphasized: “It is crucial to identify materials with large quadratic electron-phonon couplings from ab initio calculations, as this has not been systematically explored.”
More information:
Zhaoyu Han et al, Quantum bipolar superconductivity from quadratic electron-phonon coupling, Physical Examination Letters (2024). DOI: 10.1103/PhysRevLett.132.226001. On arXiv: DOI: 10.48550/arxiv.2312.03844
© 2024 Science X Network
Quote: High temperature superconductivity: exploring quadratic electron-phonon coupling (June 20, 2024) retrieved June 20, 2024 from https://phys.org/news/2024-06-high-temperature-superconductivity-exploring-quadratic.html
This document is subject to copyright. Except for fair use for private study or research purposes, no part may be reproduced without written permission. The content is provided for information only.