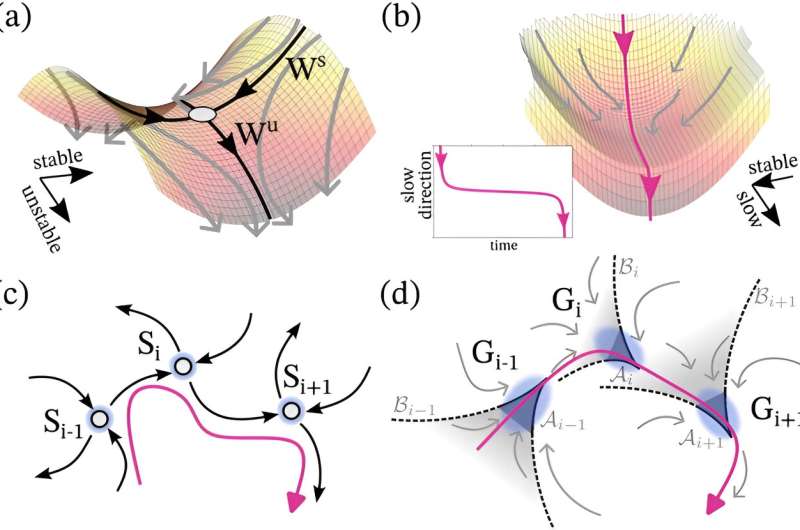
Schematics of phase-space objects. (a) Quasi-potential landscape of a saddle fixed point. Gray point: unstable location of the fixed point. (b) Quasi-potential landscape of a phantom state. Note the absence of a fixed point. Inset: time evolution of a trajectory with slow transition through the phantom. Schematic diagrams of connected saddle scaffolds (c) (𝑆𝑖), i.e. the heteroclinic channel, and (d) the ghosts (𝐺𝑖), i.e. phantom channel.𝑖 denotes the set attracting the ghosts of 𝐺𝑖and 𝐵𝑖 its basin. (a)–(d) The black, gray and magenta arrows represent respectively the (un)stable varieties, the flow direction and examples of trajectories. Credit: Physical Exam Letters (2024). DOI: 10.1103/PhysRevLett.133.047202
Scientists around the world use modeling approaches to understand complex natural systems such as climate systems or neural or biochemical networks. A team of researchers has developed a new mathematical framework that explains, for the first time, a mechanism behind long-term transient behaviors in complex systems.
They introduce ghost channels and ghost cycles as new objects that explain how natural systems can be stable over extended periods of time, yet be able to rapidly transition to another state.
This new approach challenges the traditional concept based on stable or unstable equilibria and could help us better understand how transiently stable neuronal dynamics govern the processing of sensory information, or how to potentially predict tipping cascades, such as those leading to biodiversity loss.
The joint study by the Max Planck Institute for Behavioural Neurobiology-CESAR, the University of Leicester and King’s College London was published in the journal Physical Exam Letters.
When you are in a new city and ask for directions, your working memory temporarily retains information such as turns or landmarks, which you follow in a specific order. Once you arrive at your destination, you will forget the details. To perform this task, the neural networks in your brain have opposing abilities: temporarily stabilizing neural activity in order to memorize information, but also quickly switching to a different state in the sequence.
Similar dynamics can also be observed in ecology. In competing microbial populations, one species often dominates for a long time and seems to define a stable equilibrium when, suddenly, for no apparent reason, another species takes over, causing the previous species to decline. Such transitions can even lead to extinctions and loss of biodiversity.
In order to predict whether and when such a tipping event might occur, the observed dynamics before the tipping is often analyzed. The difficulty with such predictions is that they require prior knowledge of the stability of the state or its transient nature, in order to successfully interpret the statistics of the recorded data.
However, for economically important ecosystems such as coral reefs, it is necessary to identify whether reefs that appear to be a healthy ecosystem are actually at risk of tipping into a degraded, algae-dominated state.
Challenging traditional dynamic models
Classically, the dynamical states of any complex system have been described as attractors or equilibria, abstract mathematical objects that are supposed to be observed for an infinitely long period of time and to which the system returns after a small perturbation. These states, however, do not account for how transient stability and rapid transitions can be achieved.
To introduce these two features, dynamic saddle sequences were previously considered. Similar to the shape of a saddle, it stabilizes the dynamics along one dimension (along the seat), but is inherently unstable and can fall along the orthogonal dimension.
Therefore, if the unstable dimension of one is connected to the stable dimension of another saddle, a saddle channel, called a heteroclinic channel, can emerge, such that the dynamics of the systems can switch between states in a sequence.
In a study led by scientists from the Max Planck Institute for Behavioural Neurobiology in Bonn (MPINB), in collaboration with researchers from the University of Leicester and King’s College London, the team has now demonstrated that heteroclinic channels cannot fully capture the dynamics observed in noisy real-world systems. The ability to generate transiently stable states along the saddle is lost as soon as the system encounters even minimal perturbations.
Instead, they identified special types of instabilities, called ghost channels and ghost cycles, which explain how complex systems can exhibit transiently stable and robust behavior, after which they would quickly transition to another transiently stable state that can have very different properties.
Ghost structures are a feature that appears at criticality, when a system is in equilibrium at the boundary between two or more qualitatively different regimes. Such an organization allows systems to exploit qualitatively different regimes and thus to efficiently balance opposing characteristics.
Dr. Akhilesh Nandan of MPINB explains: “By replacing the framework in which dynamics is governed by stable states, or attractors, with one in which dynamics is dictated by formally unstable structures such as ghost-based scaffolds, we were able to obtain a potential description of what has been observed experimentally in a wide range of systems. The mathematical characterization of these abstract ghost objects was crucial in defining this framework.”
Understanding ecosystem degradation or climate change
In their publication, the scientists demonstrate that ghost-based scaffolds better capture the properties of long transients in noisy systems compared to traditional models. Instead of relying on precise knowledge or the existence of (un)stable fixed points, this new framework focuses on slow directed flows organized by ghost ensembles in ghost channels and ghost cycles.
An interesting finding from this study is that ghost structures seem to highlight many different processes in biological and natural systems once you know what to look for.
“We identified ghost channels in models relevant to cell fate decisions during development, but also models of tipping cascades in climate systems that are used to explore how tipping, for example, of the Atlantic Meridional Overturning Circulation (AMOC), could affect the dynamics of other climate subsystems,” explains Dr. Daniel Koch.
These new findings therefore open many doors for future research, ranging from a theoretical understanding of how neural networks encode smell or taste, to potentially better prediction of changes in ecosystems or climate.
“What excites us most is the potential that this powerful theoretical framework can bring to research in biology and artificial intelligence,” says Dr. Aneta Koseska, who heads the Cellular Computation and Learning group at MPINB Bonn. “We have already started to investigate how phantom scaffolds can facilitate the learning of natural and artificial neural networks, and use them to overcome the current obstacles of catastrophic forgetting.”
This framework could therefore potentially provide a potential framework for studying long-lived transients, but also for identifying the limitations of current mathematical frameworks and areas where new extensions are needed to tackle long-standing open questions of quasi-steady transient dynamics in living systems, both natural and artificial.
More information:
D. Koch et al., Ghost channels and ghost cycles guiding long transients in dynamical systems, Physical Exam Letters (2024). DOI: 10.1103/PhysRevLett.133.047202
Provided by the Max Planck Society
Quote:Balancing Instability and Robustness: A New Mathematical Framework for the Dynamics of Natural Systems (2024, July 26) retrieved July 27, 2024 from https://phys.org/news/2024-07-instability-robustness-mathematical-framework-dynamics.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no part may be reproduced without written permission. The content is provided for informational purposes only.